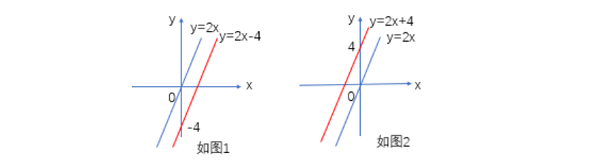
对一次函数平移规律的再探究

      我们对数学知识的理解，不能仅仅满足于其局部的应用层面，而是要追求真正的理解，做到数学思想的统一性和知识结构的完整性。对于一次函数图像的平移规律，初二绝大多数学生就能熟练的运用“左加右减，上加下减”这种固定式的模式，后进生对一次函数平移也可以找到自豪感。对于“上加下减”，学生在课堂上是很坦然地接受了，但对于“左加右减”与数轴上“左-右+”的知识有认知冲突，学生就困惑了，而且有  不少同学提出质疑。那对于一次函数左右平移的“左加右减”该不该在初二讲？要讲到什么程度呢？

      经过多年来的教学经验和教学记录，我把这些作了一些整理，仅仅是自己想理清教学上的一些“小坑”，希望能得到老师们的批评和指正。

      一、心中有图像，笔下有方法

      数学家华罗庚说过：“数缺形时少直觉，形缺数时难入微”。学习一次函数就要学会运用数形结合思想，将函数图像在脑中玩转，因此，一次函数的图像除了让学生学会通过画表格、描点、连线画出图形，还要学会根据y=kx+b中k、b的正负性迅速画出草图，并且能借助原图分析，这样才能为一次函数平移问题提供直观性，能快速验证问题的正确性。

       图形的平移，其本质是点的平移。学生对点左右、上下平移的规律要掌握好，例如：点（x,y)向左平移a个单位，则y坐标不变，x坐标-a,即（x-a,y);点（x,y)向上平移a个单位，则x坐标不变，y坐标+a,即（x,y+a),坐标平移规律与坐标轴的有序性是一致的，即“上加下减、左减右加”。点平移后产生新的坐标，求一次函数利用待定系数法，只需两点坐标代入即可。

      二、认知有冲突，知识究根源

      (一）找坑：:图像平移初部认识

      一次函数平移先理清几个关键的知识点：图像的平移与解析式k值的关系、图像上下移的规律。

      教材中第91页例2:画出y=-6x与y=-6x+5的图像，通过直观的“数形结合”观察得出一次函数图像上下平移的初印象。“上加下减”，这与直角坐标系的原点的“上正下负”的规律是契合的。因此学生在课堂上经历过从“形”到“数”和从“数”到“形”的双向直观验证，学生顺理成章地“理解”了上下平移的规律，没有同学追问真正的几何验证和代数验证。

      (二）挖坑：制造认知冲突

      上下平移，自然想到左右平移，一些练习题也出现左右平移的问题。对于初二学生是不是超知识和能力范围了呢？其实不是的，利用待定系数法同样是可以解决左右平移问题。于是，我在这次期末复习时设计了一道左右平移的题。

      问题1:  y=2x向左平移2个单位的解析式是-----------

      学生出现了三种答案； ①y=2x-2     ②y=2x-4     ③y=2x+4

      对于①答案，错误套入上下平移规律：y=2x-2:

      对于②是由y=2(x-2)=2x-4,学生由上下平移时的x坐标不变，y坐标“上加下减”联想到左右平移时也应该是y坐标不变，x坐标进行“左减右加”，而且同学还懂得用括号（x-2),说明还是有一定的思考过程。但是有同学马上就会发现利用草图验证时很明显是错误的。

如图1

      从图像看出y=2x是向右平移得到y=2x-4,很明显与题目中的向左平移相矛盾。

      对于③是y=2x+4这个答案，引导学生先用学过的知识和方法进行验证。

      学生一：图像法。如图2,  y=2x是向左平移得到y=2x+4,方向与题目是相一致的。

      学生二：待定系数法。仅靠草图判断正确性是不够严谨的，此时可利用待定系数法求出解析式。因为图像与x轴的交点为（0,0),交点（0,0)向左平移2个单位为（-2,0),设平移后的解析式为y=2x+b,把（-2,0)代入上式子得b=4,所以解析式为y=2x+4.验证得出：y=2x向左平移2个单位的解析式是y=2x+4.

      为了总结出左右平移的规律，我又在黑板上写下第二个问题。

      问题2:  y=2x向右平移3个单位的解析式是----------------------

      学生有了上面的经验，能快速利用待定系数法求得y=2x-6。

      总结得出：y=2x向左平移2个单位得y=2(x+2)即y=2x+4

      y=2x向右平移3个单位得y=2(x-3)即y=2x-6

      即一次函数左右平移时，因变量y不变，自变量x进行“左加右减”。

      (三）跳坑：解决认知冲突

      不少学生：直角坐标系内点的平移规律是“向左平移横坐标减，向右平移横坐标加”，而函数的图像是由点组成的，相对应函数图像的左右平移也应该是这个规律，为什么刚好相反呢？

      老师：对于函数左右平移“左加右减”应该是很多同学的疑惑。数轴的有序性让我们习惯于向右移动是x在增大，向左平移时x在减小，而跟函数平移却是“左加右减”好像存在矛盾，为什么会这样呢？

      问题3:  y=2x与y=2(x+2)之间的平移，为什么是向左平移了2个单位呢？解释如下：

      当x=m时，y=2x的函数值为y=2m.

      当x=m-2时，y=2(x+2)的函数值也为y=2m。

      也就是说，y=2x在x=m时的函数值与y=2(x+2)在x=m-2时的函数值相等，这时坐标的变化点（m,2m)与点（m-2,2m)的关系是：点（m.2m)向左平移2个单位得到点（m-2.2m)。可见，y=2(x+2)的图像可看作是由y=2x的图像向左平移2个长度单位得到的。

      问题4:类比解释：y=-3(x-1)向右平移4个单位得到y=-3(x-5)。同理，当y=-3(x-1)与y=-3(x-5)有相同的y，y=-3(x-1)的整体（x-1)与y=-3(x-5)的整体（x-5)要对应相等，则y=-3(x-5)的x要比y=-3(x-1)中的x大4.即坐标向右平移平移4个单位。那么图像也会向右平移4个单位。以此类推，从而阐释了一次函数平移“左加右减”规律的本质。

      (四）出坑：旧知识继续追问

      课后有学生马上就反思追问，观察图像得到的规律不够严谨，提出了以下问题：

      ①平移中的“上加下减”的本质是什么，能用上面的方法来解释吗？

      ②平移k相等，垂直k相乘等于-1.只是靠图像法得到的规律也是不严谨，若要有严谨的证明该怎么证明？

      因为要用到初三一些知识，我建议学有余力的同学可以相互之间探讨，也可以初三再继续研究。由左右平移问题点燃学生对理所当然的“知识点”的再思考，促使他们对认知冲突的点进行聚焦和深度反思，真正学懂数学。

     三、教学深思考，反思再出发

      回想以前用固定式的思维“上加下减、左加右减”方式讲给学生，只是通过画图象来总结规律，这种单一的传授方法是缺少深度思考的。

      一是在挖坑阶段（上加下减）,学生没有追问为什么，可能居于知识的有限，但我觉得更多是平时自己在教学中没有培养好学生用数学的思维来思考问题。

      二是在跳坑阶段（解决认知冲突）时，因为有些方法不适合在初二讲，但是学生一旦提出来，作为学生的指导者，我们教师要知其然知其所以然，并能用学生能接受的方法解析。

      三是函数左右平移在初三的二次函数才牵涉到，但在初二课堂自动生成的，应该和学生分享方法和知识的来源，而且要鼓励学生大胆质疑、善于用数学思维来思考问题，多问为什么，从哪里来，到哪去。让学生认识到一个公式、定理、规律都是用根据已知的事实或原理，合乎逻辑地推出结论，构建数学的逻辑体系，形成重论据、有条理、合乎逻辑的思维。

      作者 ：四川省巴中市兴合实验学校  冯博