|
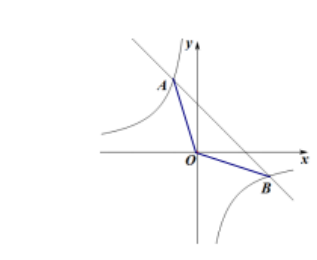
一题一作业实践探究——以《双曲线与直线的综合》作业为例时间:2024-07-02 在“双减”政策出台背景下,如何合理调控及优化设计作业,以达到减少重复题型训练,实现作业预期价值,促进学生有效发展。本文通过一题多问的形式设计,立足于每一问之间的层层递进,有助于学生跨越最近发展区,理清同一个知识与不同知识之间的综合联系,减少阅读题目时间,加强作业题目之间的联系,减量提质。 作业呈现: C组 1.如图,一次函数y1=kx+b的图像与反比例函数y2=
(1)求点A、B的坐标 (2)求一次函数解析式。 (3)求出直线y1=kx+b与x轴、y轴的交点坐标, 以及围成的三角形面积。 B组 (4)若y1>y2,则x的取值范围是—— (5)若直线y1=kx+b与y轴相交于点C,求△AOC、△AOB的面积。 (6)在双曲线上找一点P,使△OCP是△OCA面积的2倍,求点P坐标; (7)在y轴上找一点E,使得△AEB是△AOB面积的3倍,求点E坐标 A组 (8)如图,若点F是x轴的一动点,当△AOF是等腰三角形时,求点F坐标。 (9)请根据本题,再设计一小问,并解答。 设计反思: 一、选题,编排 《双曲线与直线的综合》是在学完《反比例函数的图像与性质》后学习的一个重点也是一个热点内容。由于学生基础差异较大,很多同学尚处于知识“消化”当中。为了更准确的了解学生真实学习情况,我让学生进行作业设计,由各个等级的学生选出C、B、A三个层次的作业题目,发现基础薄弱的同学主要选择交点问题、解析式问题、简单的三角形面积问题,中等学生主要选择求自变量取值,比较函数值大小问题、复杂的面积问题,优等生主要选择等腰三角形的存在问题等。综合学生学情,我将这些题目融合编排成一道题,一题多问。既节省了不必要的机械刷题,又激发了学生的追问思维。由易到难,层层递进,为学生创建最近发展区,让学生在连环的一问一问中探索解题方法和思想,让题目的难度步步降低,也培养了学生发现问题,提升问题,分析问题和解决问题的能力。让学生体会转化和化归思想,归纳梳理出解决问题的模型。 二、变式,探究 第(5)问求△A0C、△AOB的面积。如果直接求△AOB面积,已掌握的同学习惯沿着x轴将△AOB割成两个三角形,此时两个三角形的高皆为各自的lyl.但学生基本对此已掌握。而对三角形高为|x|的难以理解。纵观双曲线与直线综合,在求三角形面积最值时,大都需要用平行于y轴的直线进行“切割”。所以先求△AOC可以帮助学生掌握求高为|x|的三角形面积,也“提醒”学生将△AOB沿着y轴“切割”。第(6)、(7)问分别是求△AOC、△AOB的变式与升华,让学生感受到点由静到动、由数到字母的跨越,也找到了解决这一类问题的基本模型,进一步培养学生转化与化归的能力。 三、反馈,分析 每一次设计作业,除了要专研教材,考点,更应该要专研学生的最新现状,作业布置后,了解学生最新的作业情况,了解学生弱项,有的放矢,再做调整。 (一)本以为学生对第(3)小题这种由数到形利用函数图像解不等式很容易,但其实学生很难理解:有些学生甚至弄不清楚是要求x的取值范围还是求y的取值范围,有些学生看不出哪个函数图像在上面,有些同学不知道要跳过哪个点…… (二)在求△AOB的面积时,学生存在不知道如何“切割”三角形,缺乏对三角形要“横割”或“竖割”的思想意识,因为没有标出直线与x轴或y轴的交点,也限制了学生“割”的思维。 (三)对于题(5),学生对动点有一种畏惧心理,有部分学生因为见到动点而就放弃,没有看题目去深入思考。因为点p是一个动点,学生不知如何表达三角形的高,也不清楚需要如何分类,以何分类,没有借鉴前几问的结论。 (四)对于题(7),在分类的时候,学生大多以腰分类,但是容易混乱,错漏。在计算的时候没有利用好等腰三角形的性质而求得点。 (五)题(8)完成的人数较少,老师可以上课讲解,学生订正完成。最后一问以作业的形式出了一道开放式的题目,让学生自己通过已有条件,自设问题,自己作答,既考察了学生已掌握的运算知识和技巧,也促进学生发散思维的发展,提高学生数学综合能力。当然,作者更倾向于将数学与实践相结合,通过学习数学知识解决实际问题,让学生清晰感受数学的价值,让学习数学成为一种需求,这样一种内在动力将持久的驱动学生努力学习数学知识,这将是一种趋势,也是我们不断努力的目标! 作者:巴中市兴合实验学校 冯博 |


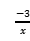 的图像相交于A(-1,m)、B(n,-1)两点,连接OA、OB。
的图像相交于A(-1,m)、B(n,-1)两点,连接OA、OB。